

The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). Regression line for 50 random points in a Gaussian distribution around the line y=1.5x+2 (not shown).
#Google excel linear regression line standard error formula series#
GROWTH: Given partial data about an exponential growth trend, fits an ideal exponential growth trend and/or predicts further values.Set of statistical processes for estimating the relationships among variables Part of a series on LOGEST: Given partial data about an exponential growth curve, calculates various parameters about the best fit ideal exponential growth curve. TREND: Given partial data about a linear trend, fits an ideal linear trend using the least squares method and/or predicts further values. The degrees of freedom, useful in looking up F statistic values in a reference table to estimate a confidence level, The F statistic, or F-observed value indicating whether the observed relationship between dependent and independent variables is random rather than linear, Standard error for the dependent variable values, The coefficient of determination (between 0 and 1, where 1 indicates perfect correlation), The standard error for each coefficient and the intercept, If verbose is TRUE, in addition to the set of linear coefficients for each independent variable and the y-intercept, LINEST returns Verbose - A flag specifying whether to return additional regression statistics or only the linear coefficients and the y-intercept (default).

forces the curve fit to pass through the origin. Otherwise, forces b to be 0 and only calculates the m values if FALSE, i.e. if known_data_y is a single row, each row in known_data_x is interpreted as a separated independent value, and analogously if known_data_y is a single column.Ĭalculate_b - Given a linear form of y = m*x+b, calculates the y-intercept ( b) if TRUE.

if known_data_y is a single row, each row in known_data_x is interpreted as a separated independent value, and analogously if known_data_y is a single column. If known_data_y is a one-dimensional array or range, known_data_x may represent multiple independent variables in a two-dimensional array or range. If known_data_y is a two-dimensional array or range, known_data_x must have the same dimensions or be omitted. Known_data_y - The array or range containing dependent (y) values that are already known, used to curve fit an ideal linear trend.
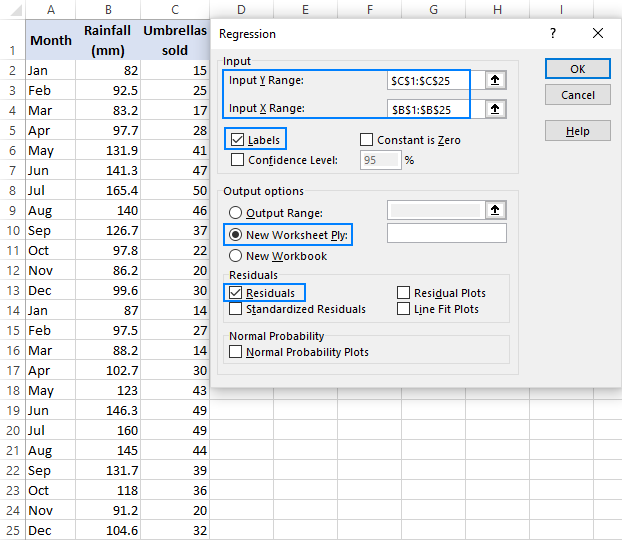
LINEST(B2:B10, A2:A10, FALSE, TRUE) Syntax Given partial data about a linear trend, calculates various parameters about the ideal linear trend using the least-squares method.


 0 kommentar(er)
0 kommentar(er)
